使用 DGL 进行批量图分类
图分类是一个重要的问题,在许多领域都有应用,包括生物信息学、化学信息学、社交网络分析、城市计算和网络安全。最近,将图神经网络应用于此问题已成为一种流行的方法(Ying 等,2018,Cangea 等,2018,Knyazev 等,2018,Bianchi 等,2019,Liao 等,2019,Gao 等,2019)。
本教程演示了
- 如何使用 DGL 批量处理大小和形状各不相同的多个图
- 如何训练图神经网络用于一个简单的图分类任务
简单的图分类任务
在本教程中,我们将通过一个玩具示例(对如下所示的 8 种类型的正则图进行分类)来学习如何使用 DGL 执行批量图分类

我们在 DGL 中实现了这个微型图分类数据集。该数据集包含 8 种不同类型的图,每个类都有相同数量的图样本。
from dgl.data import MiniGCDataset
import networkx as nx
# a dataset with 80 samples, each graph is
# of size [10, 20]
dataset = MiniGCDataset(80, 10, 20)
graph, label = dataset[0]
nx.draw(graph.to_networkx())
print('Class:', label)
形成图 mini-batch
为了更有效地训练神经网络,一种常见做法是将多个样本批量处理在一起形成一个 mini-batch。批量处理固定形状的张量输入相当容易(例如,批量处理两张 28x28 大小的图像会得到一个形状为 2x28x28 的张量)。相比之下,批量处理图输入有两个挑战
- 图是稀疏的。
- 图可以有不同的长度(例如,节点和边的数量)。
为了解决这个问题,DGL 提供了 dgl.batch API。它利用了将一批图视为一个包含许多不相交连通分量的大图的技巧。下面是一个可视化图,给出了大致思路

例如,我们可以定义以下 collate 函数,从给定的图和标签对列表(由 MiniGCDataset 提供)形成一个 mini-batch
def collate(samples):
# The input `samples` is a list of pairs
# (graph, label).
graphs, labels = map(list, zip(*samples))
batched_graph = dgl.batch(graphs)
return batched_graph, torch.tensor(labels)
dgl.batch 的返回类型仍然是一个图(类似于一批张量仍然是一个张量的原理)。这意味着任何适用于单个图的代码都可以立即用于一批图。更重要的是,由于 DGL 并行处理所有节点和边上的消息,这极大地提高了效率。
图分类器
图分类可以按以下步骤进行

从一批图中,我们首先对节点执行消息传递/图卷积,使它们“相互通信”。消息传递后,我们根据节点(和边)属性计算用于表示图的张量。此步骤可以互换地称为“读出/聚合”。最后,将图表示输入分类器以预测图标签。
图卷积
我们的图卷积操作基本上与 GCN 的相同(请查看我们之前的GCN 教程)。唯一的区别是我们用替换。用平均代替求和是为了平衡不同度数的节点,这在此实验中提供了更好的性能。
请注意,在数据集初始化中添加的自环边允许我们包含原始节点特征在取平均值时。下面是在 DGL 中实现此 GCN 的代码片段。
import dgl.function as fn
import torch
import torch.nn as nn
# Sends a message of node feature h.
msg = fn.copy_src(src='h', out='m')
def reduce(nodes):
"""Take an average over all neighbor node features hu and use it to
overwrite the original node feature."""
accum = torch.mean(nodes.mailbox['m'], 1)
return {'h': accum}
class NodeApplyModule(nn.Module):
"""Update the node feature hv with ReLU(Whv+b)."""
def __init__(self, in_feats, out_feats, activation):
super(NodeApplyModule, self).__init__()
self.linear = nn.Linear(in_feats, out_feats)
self.activation = activation
def forward(self, node):
h = self.linear(node.data['h'])
h = self.activation(h)
return {'h' : h}
class GCN(nn.Module):
def __init__(self, in_feats, out_feats, activation):
super(GCN, self).__init__()
self.apply_mod = NodeApplyModule(in_feats, out_feats, activation)
def forward(self, g, feature):
# Initialize the node features with h.
g.ndata['h'] = feature
g.update_all(msg, reduce)
g.apply_nodes(func=self.apply_mod)
return g.ndata.pop('h')
读出和分类
在此演示中,我们将初始节点特征视为其度数。经过两轮图卷积后,我们通过对批次中每个图的所有节点特征进行平均来执行图读出
在 DGL 中,dgl.mean_nodes(g) 为一批可变大小的图处理此任务。然后,我们将图表示输入到一个包含一个线性层和 的分类器中.
import torch.nn.functional as F
class Classifier(nn.Module):
def __init__(self, in_dim, hidden_dim, n_classes):
super(Classifier, self).__init__()
self.layer0 = GCN(in_dim, hidden_dim, F.relu)
self.layer1 = GCN(hidden_dim, hidden_dim, F.relu)
self.classify = nn.Linear(hidden_dim, n_classes)
def forward(self, g):
# For undirected graphs, in_degree is the same as
# out_degree.
h = g.in_degrees().view(-1, 1).float()
h = layer0(g, h)
h = layer1(g, h)
g.ndata['h'] = h
hg = dgl.mean_nodes(g, 'h')
return self.classify(hg)
设置和训练
我们创建了一个包含 1000 个图的合成数据集,每个图有 10 到 20 个节点。
from torch.utils.data import DataLoader
import torch.optim as optim
from dgl.data import MiniGCDataset
# Create training and testing set.
trainset = MiniGCDataset(1000, 10, 20)
testset = MiniGCDataset(200, 10, 20)
# Use pytorch's DataLoader and the collate function
# defined before.
data_loader = DataLoader(trainset, batch_size=32, shuffle=True,
collate_fn=collate)
# Create model
model = Classifier(1, 32, 8)
loss_func = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)
model.train()
epoch_losses = []
for epoch in range(50):
epoch_loss = 0
for iter, (bg, label) in enumerate(data_loader):
prediction = model(bg)
loss = loss_func(prediction, label)
optimizer.zero_grad()
loss.backward()
optimizer.step()
epoch_loss += loss.detach().item()
print('Epoch {}, loss {:.4f}'.format(epoch, loss))
epoch_losses.append(epoch_loss / (iter + 1))
下面展示了一次运行的学习曲线
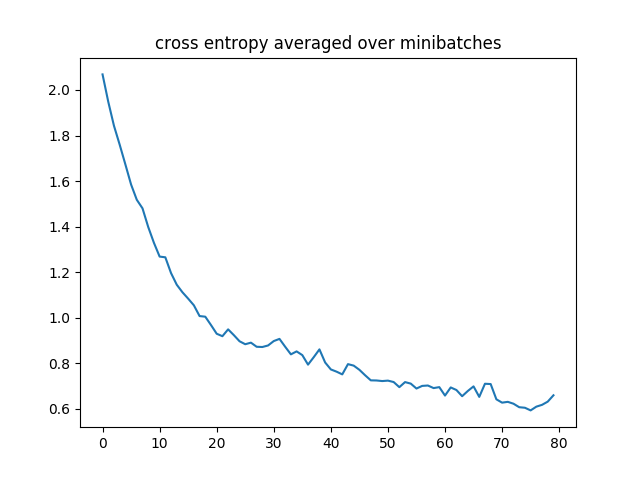
在训练好的分类器对我们的测试集进行测试时,采样预测的准确率在随机运行中介于 78% 到 85% 之间波动。argmax 准确率通常更高,可以达到 91%。
# Convert a list of tuples to two lists
model.eval()
test_X, test_Y = map(list, zip(*testset))
test_bg = dgl.batch(test_X)
test_Y = torch.tensor(test_Y).float().view(-1, 1)
probs_Y = torch.softmax(model(test_bg), 1)
sampled_Y = torch.multinomial(probs_Y, 1)
argmax_Y = torch.max(probs_Y, 1)[1].view(-1, 1)
print('Accuracy of sampled predictions on the test set: {:.4f}%'.format(
(test_Y == sampled_Y.float()).sum().item() / len(test_Y) * 100))
print('Accuracy of argmax predictions on the test set: {:4f}%'.format(
(test_Y == argmax_Y.float()).sum().item() / len(test_Y) * 100))
下面是一个动画,其中我们绘制了图,并显示了训练好的模型将其真实标签分配给该图的概率

为了了解节点/图特征在训练好的模型中如何随层数变化,我们使用 t-SNE 进行降维和可视化。


顶部的两个小图分别可视化了图卷积层 #1 和 #2 后的节点特征,底部的大图可视化了图的 pre-softmax logits。如您所见,不同类型图的节点嵌入在较高层和较低层中更易于区分。最后,不同类型图的嵌入已很好地分离。
接下来是什么?
在这里下载完整的教程代码和 jupyter notebook。
使用图神经网络进行图分类仍然是一个非常年轻的领域,等待人们带来更多激动人心的发现!这并不容易,因为它需要在将不同图映射到不同嵌入空间的同时,保留其结构相似性。要了解更多信息,ICLR 2019 的论文 《图神经网络有多强大?》 可能是一个很好的起点。
关于批量图处理的更多示例,请参阅
- 我们关于 Tree LSTM 和 深度图生成模型 的教程
- Junction Tree VAE 的一个示例实现。
1 月 25 日
作者:Mufei Li,Minjie Wang,发布于 博客
